วิธีใช้
คำนวณสูตรของเคลลี่เป็นเครื่องมือในการค้นหาขนาดการลงทุนที่เหมาะสมที่สุดสำหรับผลตอบแทนสูงสุดจากการลงทุนซ้ำ เมื่อทราบอัตราต่อรองและผลตอบแทนของการลงทุน
- อัตราส่วนการชนะ : ป้อนความน่าจะเป็นที่จะได้กำไรจากการลงทุน
- กำไรที่คาดหวัง เมื่อชนะ : ป้อนอัตราผลตอบแทนที่คาดหวัง ตัวอย่างเช่น หากคุณลงทุน 100 และได้ 10 อัตราผลตอบแทนคือ 10%
- การสูญเสียที่คาดหวัง เมื่อพ่ายแพ้ : ป้อนอัตราการสูญเสียที่คาดหวัง ตัวอย่างเช่น หากคุณลงทุน 100 และสูญเสีย 10 อัตราการสูญเสียคือ 10%
สัดส่วนการลงทุนที่เหมาะสมที่สุด หมายถึงอัตราส่วนการลงทุนที่เหมาะสมสำหรับเงินทุน ตัวอย่างเช่น หากคิดเป็น 50% คุณควรลงทุน 50% ของเงินทุนในแต่ละครั้ง ในทางกลับกัน 100% หรือมากกว่าหมายถึงการลงทุนโดยใช้เลเวอเรจ
สูตรเคลลี่คืออะไร?
สูตรของ Kelly เป็นสูตรทางทฤษฎีเพื่อให้ได้ผลตอบแทนที่ดีที่สุดเมื่อนำเงินไปลงทุนซ้ำๆ การกำหนดขนาดการลงทุนของคุณตามสูตรของ Kelly สามารถให้ผลลัพธ์ที่ดีที่สุดในทางทฤษฎี
ความเสี่ยง
สูตรของ Kelly ระบุถึงความน่าจะเป็นและขนาดของผลตอบแทนจากการลงทุนอย่างชัดเจน อย่างไรก็ตาม ในการลงทุนในโลกแห่งความเป็นจริง เป็นไปไม่ได้ที่จะคาดเดาสิ่งนี้ได้อย่างเต็มที่ สูตรของ Kelly แสดงให้เห็นว่าการเปลี่ยนแปลงความน่าจะเป็นเพียงเล็กน้อยก็สามารถเปลี่ยนขนาดของการลงทุนได้อย่างมาก ดังนั้น คุณจึงไม่ควรพึ่งพาสูตรของ Kelly เพียงอย่างเดียวในการตัดสินใจลงทุน
ประโยชน์ของสูตรเคลลี่
ประโยชน์ของเกณฑ์ของ Kelly คือมันแสดงให้เห็นว่ายิ่งสินทรัพย์ที่คุณลงทุนมีความผันผวนมากเท่าไร คุณก็ยิ่งควรลดขนาดสินทรัพย์ลงมากขึ้นเท่านั้น ตัวอย่างเช่น แม้ว่าคุณจะมีอัตราส่วนกำไร/ขาดทุนเท่ากัน หากคุณลงทุนใน [ชนะ: +20% แพ้: -10%] คุณต้องลดจำนวนเงินลงทุนลงครึ่งหนึ่งเมื่อเทียบกับ [ชนะ: +10% แพ้: -5%] เพื่อให้ได้ผลลัพธ์ที่ดีที่สุด
สมการของสูตรของเคลลี่
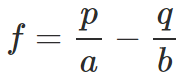
- f : สัดส่วนการลงทุนที่เหมาะสมที่สุด
- p : อัตราส่วนการชนะ
- q : อัตราส่วนพ่ายแพ้ (q = 1-p)
- a : การสูญเสียที่คาดหวัง เมื่อพ่ายแพ้
- b : กำไรที่คาดหวัง เมื่อชนะ