Cómo utilizar
Calculadora de criterio de Kelly es una herramienta para encontrar el tamaño de inversión óptimo para maximizar las ganancias en inversiones repetidas.
- Probabilidad de ganar : Introduzca la probabilidad de obtener una ganancia de su inversión.
- Ganancia de resultado positivo : Introduzca la ganancia potencial de un resultado positivo. Por ejemplo, si invierte 100 y obtiene 10, la ganancia es del 10%.
- Pérdida de resultado negativo : Introduzca la pérdida potencial de un resultado negativo. Por ejemplo, si invierte 100 y pierde 10, la pérdida es del 10%.
Proporción óptima de inversión significa el ratio de inversión ideal para el capital. Por ejemplo, si es del 50%, lo ideal es que inviertas el 50% de tu capital cada vez. Por otro lado, 100% o más significa inversiones apalancadas.
¿Qué es el Criterio de Kelly?
El Criterio de Kelly es una fórmula teórica para obtener el mejor rendimiento al invertir dinero repetidamente. Dimensionar una inversión de acuerdo con el Criterio de Kelly teóricamente puede producir los mejores resultados.
Riesgos
El Criterio de Kelly requiere claramente la probabilidad y la magnitud de un retorno de una inversión. Sin embargo, en la inversión del mundo real, es imposible predecir completamente esto. En el Criterio de Kelly, incluso un pequeño cambio en la probabilidad puede cambiar significativamente el tamaño de una inversión. Por lo tanto, no debe tomar una decisión de inversión basándose únicamente en el Criterio de Kelly.
La utilidad del criterio de Kelly
La utilidad del criterio de Kelly es que muestra que cuanto más volátil sea el activo en el que está invirtiendo, más debería reducirlo. Por ejemplo, incluso si tiene la misma relación de pérdidas y ganancias, si invierte en [Ganancia: +20%, Pérdida: -10%], necesita reducir la cantidad de inversión a la mitad en comparación con [Ganancia: +10%, Pérdida: -5%] para lograr resultados óptimos.
Fórmula del criterio de Kelly
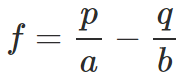
- f : Proporción óptima de inversión
- p : Probabilidad de ganar
- q : Probabilidad de perder (q = 1-p)
- a : Pérdida de resultado negativo
- b : Ganancia de resultado positivo